わ た し の 素 数 第二段階：計算候補をふるい落として高速化
あなただけの素数を探そう
最終更新日：2004-03-11 （Noharaさん作NewPGenマニュアル，拡張子に関する注意削除）
前回のやり方で、19510223*2^2+1から19510223*2^5000+1まで、24秒で素数を探索できました。
今度は19510223*2^2+1から19510223*2^20000+1まで素数を探してみましょう。
前回のやり方通りに数値を入力し、nの部分に5000と入れる代わりに20000と入れて計算してみてください。
皆さんのパソコンでは何分かかりましたか？
私のCeleron1400MHzでは13分24秒かかりました。
1000桁・2000桁の素数を探すなら問題ありませんが、Top5000にランクインする４万桁以上の素数を探すとなると、2004年2月時点で19510223*2^150000+1ぐらいを探索しないとなりません。
出来るものなら高速化したいです。
そこで、NewPGen.exeとPRP.exeを使って、proth.exeに計算させる数を、事前にふるい落として高速化してみましょう。
まずはNewPGenとproth.exeを使うやり方に挑戦してみましょう。
NewPGenは全ての素数候補の数を試し割することで、proth.exeで素数判定する前に、不要な数をふるい落としてくれます。
例によって、またThe Prime Pagesからダウンしましょう。
もちろん無料で利用できるソフトウェアです。
新規に処理する今回は、Create a new fileを選択。
出力するファイル名を「Output file:」に記載します。
*Proth.exeで読み取り時エラーが発生する可能性があるらしく、ファイル名には拡張子をつけないほうが良いそうです。
**Proth.exe Ver5.**当時の問題で、現在では拡張子をつけても問題無いそうです。
今回も19510223*2^n+1の形で探すので、「Type:」には「k.b^n+1 with k fixed」を選び、Startを押して、ふるい落とし作業を開始します。
NewPGenのふるい落とし作業は、そのまま放置していると、とんでもなく長く（proth.exeで全ての数を素数判定するよりも長く）、ふるい落とし作業をし続けてしまいます。
適当な頃合を見計らって、「Stop」を押して、ふるい落とし作業を終了させましょう。
しかし、「適当な頃合」とは、どれくらいなのでしょう？
私にもまだ掴めないのですが、今回は19510223*2^20000+1までと、まだ小さいので、1〜２秒程でStopしてみましょう。
Stopさせると「Output file:」に入力したファイル名のファイル（この例では「19510223n2n20000」）がNewPGen.exeのあるフォルダと同じ場所に生成されているはずです。
この「19510223n2n20000」ファイルを、今度はProth.exeに読み込ませて、素数判定させましょう。
もし、もう一段、別のふるい落とし作業を行って更に素数判定の効率を高めたい場合は「NewPGenでふるい落とした数を、更にPRPでフェルマーテストにかける」に進みましょう。
NewPGenがふるい落とした数だけを、proth.exeに素数判定させる
|
proth.exeを実行します。
proth.exeだけを使う場合は手動で数の範囲を入力しましたが今回は違います。
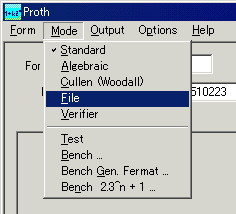
NewPGenがふるい落とした数だけを素数判定するので、Mode → Fileで、ファイル名入力モードにします。
あ、そうそう、NewPGenとproth.exeとが別々のフォルダに存在するなら、NewPGenによって出力された「19510223n2n20000」ファイルをproth.exeの存在するフォルダにコピーしておいて下さい。
そしてもう１つ、探す素数のタイプを前回と同様、Form → k.2^n+1と選んでください。
これがファイル名入力モードです。
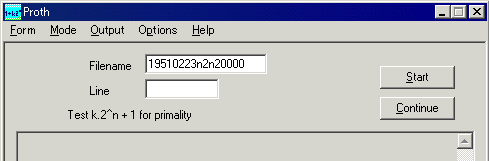上のようにNewPGenで「Output file:」に入力したファイル名を入れてStartボタンをクリックします。
これでようやく素数判定スタートです。
今回の結果は、こうなりました。
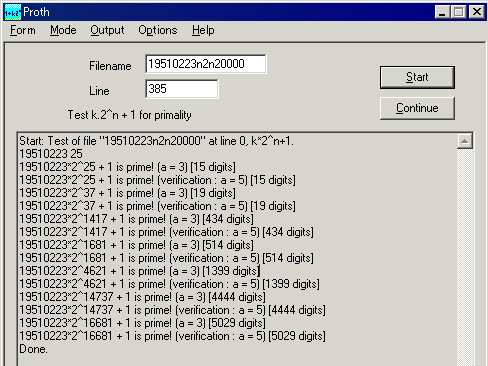Celeron1400MHzでは、探索にかかった時間はproth.exeだけで12分46秒でした。
NewPGenの処理に2秒かけたとして、トータルの計算時間は12分48秒です。
proth.exe単体の13分24秒と比べると、40秒短縮に成功しました。
NewPGenでふるい落とした数を、更にPRPでフェルマーテストにかける
|
先程はNewPGen → proth.exeで1回ふるい落としただけでした。
今回は、NewPGen → PRP.exe → proth.exeと、ふるい落とした後、フェルマーテストにかけた後、本判定することで、更に効率よく素数判定を行います。
まずはPRPをダウンロード（Windows版ダイレクトリンク）しましょう。
余談ですがPRPはGIMPSのGeorge Woltman氏制作なので、GIMPSのmersenne.orgサーバからのダウンロードとなります。
「まず最初にNewPGenを使って試し割」の項目通りに、NewPGenから「Output file:」である「19510223n2n20000」ファイルを生成します。
次にPRPを実行します。
PRPは、フェルマーテスト（素数判定したい数Nに対し、それと素であるaとa^(n-1)=1 (mod n)が成り立たない時、Nは合成数である。99.9%以上の確率で判定可能。）を行うソフトです。
PRPは実行するとタスクトレイにいるので、ダブルクリックしてウインドウにして下さい。
Test → Input Data...で、ファイル名入力モードにしましょう。
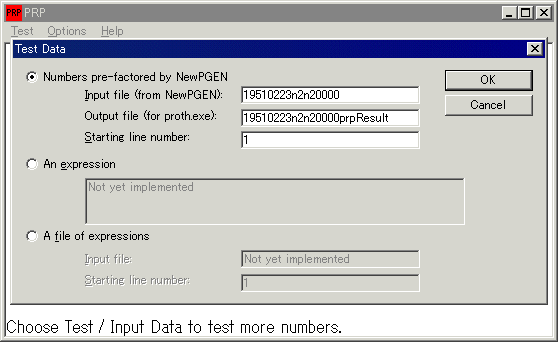「Input file(from NewPGEN):」には、NewPGenで生成したファイル名「19510223n2n20000」を。
「Output file (for proth.exe):」には、出力するファイル名を記載します。（この例では19510223n2n20000prpResult）
Starting line numberは、私もよく理解していないのですが、1のままでいいそうです。
入力が終わったらOKをクリックして、フェルマーテストを始めましょう。
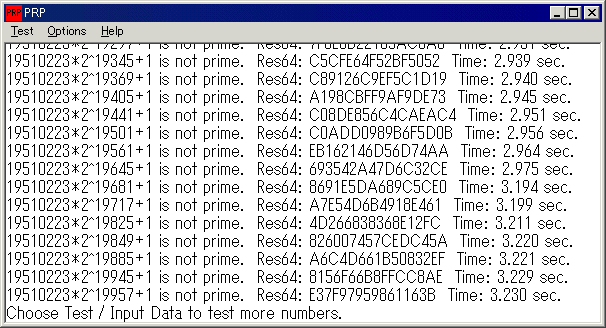PRPのフェルマーテストが終了しました。
celeron1400MHzで6分14秒かかりました。
生成された「19510223n2n20000prpResult」をメモ帳などのエディタで見てみると判りますが、6つの数が記載されています。
これがフェルマーテストによって残った素数候補です。
とはいえ前述の通りフェルマーテストは100%完全に素数判定できるわけではありません。
PRPが生成した「19510223n2n20000prpResult」ファイルを、proth.exeに読み込ませて素数判定しましょう。
NewPGenでふるい落として更にPRPで仮判定した数を、proth.exeで素数判定
|
「NewPGenがふるい落とした数だけを、proth.exeに素数判定させる」の項目のように、proth.exeを実行し、Mode → Fileで、ファイル名入力モードにします。
PRPが生成した「19510223n2n20000prpResult」ファイルとproth.exeとが別々のフォルダに存在するなら、「19510223n2n20000prpResult」ファイルをproth.exeと同じフォルダにコピーしておいて下さい。
探す素数のタイプは今回も、Form → k.2^n+1と選択。
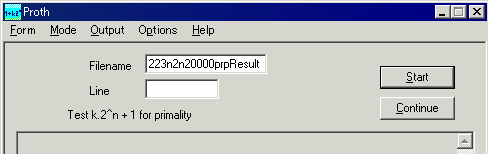「Filename」欄に、PRPが出力したファイル名「19510223n2n20000prpResult」と記入し、Startを押せば、ついに素数判定スタートです。
Celeron1400MHzでは、今回探索にかかった時間はproth.exeだけで41秒でした。
NewPGenの処理に2秒，PRPに6分14秒かけたので、トータルの計算時間は6分57秒です。
proth.exe単体の13分24秒と比べると、6分27秒短縮に成功しました。
NewPGen2秒＋proth.exeで合計12分48秒と比べても、5分51秒短縮に成功しました。
効果覿面ですね。
「まず最初にNewPGenを使って試し割」の項では、２秒程でNewPGenのふるい落とし作業を終了しました。
巨大素数の探索においては、どれくらいの時間、ふるい落とすのが適切なのでしょう。
NewPGenでふるい落とし作業を始めて30秒ほどすると、ウインドウの一番下に、
Rate : ** n's per second
という表示が出てきます。
これは、直近10秒中、1秒あたり**個の数を、素数候補から ふるい落としたという意味です。
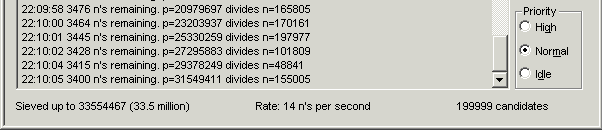上の例では1秒あたり14個ですが、時間が経つに連れて、多くの素数候補をふるい落とし終わり、
Rate : 13 n's per second （1秒あたり13個）
Rate : 12 n's per second （1秒あたり12個）
．．．
と、次第に小さくなり、いずれ「1秒あたり1個」を切ってしまいます。
ふるい落とすペースが、どんどん落ちていってしまうわけです。
「1秒あたり1個ふるい落とす」よりも遅くなると、下記のようになります。
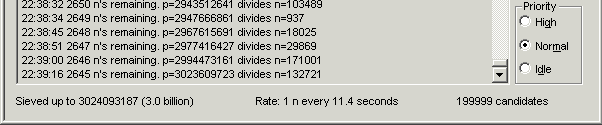Rate : 1 n every ** secondsは、1個の数を、素数候補から ふるい落とすのに**秒かかっているという意味です。
上の例では1個あたり11.4秒かかっています。
ふるい落とし作業が進めば進む程、より1個の数をふるい落とすのにかかる時間が長くなっていきます。
そこで、
１．PRP.exeやproth.exeで実際に1つの数を素数判定するのにかかる時間より、NewPGenで1つの数をふるい落とすのにかかる時間が短い状態まではNewPGenを使う。
２．NewPGenで1つの数をふるい落とすのにかかる時間が、PRP.exeやproth.exeで実際に1つの数を素数判定するのにかかる時間より長くなったらNewPGenを終了して、PRP.exeやproth.exeによる素数判定作業に移る。
というのが、一つの判断基準になれそうです。
素数探索のいろはを私に教えてくださった野原さんは、現在k*2^530000+1辺り(16万桁)の数の素数判定をされているそうですが、p=1000000000000(１兆）辺りまで、ふるいを実施すると、PRP.exeのバトンタッチラインになるそうです。
この場合、NewPGenによる、ふるい作業だけで１、２週間かけておられるそうです。
・NewPGen.exeマニュアル このソフトをより使いこなすには（Noharaさん作）
いつもお世話になっているNoharaさんに、NewPGenの詳細マニュアルを作っていただきました。
NewPGenをより詳しく知ることができます。
Noharaさん、ありがとうございました。掲載等、いつもこちらの対応遅れてすみません。
このページを作るにあたって、Proth.exeに続いて、NewPGen，PRPの日本語での詳細な情報の提供など、野原さんからの多大なご支援・ご協力を頂きました。
当ページのほとんどの情報は、野原さんがもたらしてくれた情報をベースに作られています。
野原さんがいなければ、私には個々のソフトウェアの機能の意味すら理解できていなかったのではと思います。
ありがとうございました。
情報のご提供，このページに間違い等ありましたらMat(mat-t@mh1.117.ne.jp)か掲示板（旧）までご指摘頂ければありがたいです。
・Top - back - The Prime Pagesの歩き方 - 素数探索連携掲示板 - 分散コンピューティングの紹介 - GIMPS - 世界最大の素数を求め続ける
・Mat (mat-t@mh1.117.ne.jp)